本文共 10880 字,大约阅读时间需要 36 分钟。
首先上一段cubemx导出的freertos的配置文件,这个配置文件是cubemx导出生成的。芯片是stm32f103zet6,(freertos代码风格是在是比较差,尤其是名称,看ucos爽多了)
/* FreeRTOS V9.0.0 - Copyright (C) 2016 Real Time Engineers Ltd. All rights reserved VISIT http://www.FreeRTOS.org TO ENSURE YOU ARE USING THE LATEST VERSION. This file is part of the FreeRTOS distribution. FreeRTOS is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License (version 2) as published by the Free Software Foundation >>!AND MODIFIED BY!<< the FreeRTOS exception. *************************************************************************** >>! NOTE: The modification to the GPL is included to allow you to !<< >>! distribute a combined work that includes FreeRTOS without being !<< >>! obliged to provide the source code for proprietary components !<< >>! outside of the FreeRTOS kernel. !<< *************************************************************************** FreeRTOS is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. Full license text is available on the following link: http://www.freertos.org/a00114.html *************************************************************************** * * * FreeRTOS provides completely free yet professionally developed, * * robust, strictly quality controlled, supported, and cross * * platform software that is more than just the market leader, it * * is the industry's de facto standard. * * * * Help yourself get started quickly while simultaneously helping * * to support the FreeRTOS project by purchasing a FreeRTOS * * tutorial book, reference manual, or both: * * http://www.FreeRTOS.org/Documentation * * * *************************************************************************** http://www.FreeRTOS.org/FAQHelp.html - Having a problem? Start by reading the FAQ page "My application does not run, what could be wrong?". Have you defined configASSERT()? http://www.FreeRTOS.org/support - In return for receiving this top quality embedded software for free we request you assist our global community by participating in the support forum. http://www.FreeRTOS.org/training - Investing in training allows your team to be as productive as possible as early as possible. Now you can receive FreeRTOS training directly from Richard Barry, CEO of Real Time Engineers Ltd, and the world's leading authority on the world's leading RTOS. http://www.FreeRTOS.org/plus - A selection of FreeRTOS ecosystem products, including FreeRTOS+Trace - an indispensable productivity tool, a DOS compatible FAT file system, and our tiny thread aware UDP/IP stack. http://www.FreeRTOS.org/labs - Where new FreeRTOS products go to incubate. Come and try FreeRTOS+TCP, our new open source TCP/IP stack for FreeRTOS. http://www.OpenRTOS.com - Real Time Engineers ltd. license FreeRTOS to High Integrity Systems ltd. to sell under the OpenRTOS brand. Low cost OpenRTOS licenses offer ticketed support, indemnification and commercial middleware. http://www.SafeRTOS.com - High Integrity Systems also provide a safety engineered and independently SIL3 certified version for use in safety and mission critical applications that require provable dependability. 1 tab == 4 spaces!*/#ifndef FREERTOS_CONFIG_H#define FREERTOS_CONFIG_H/*----------------------------------------------------------- * Application specific definitions. * * These definitions should be adjusted for your particular hardware and * application requirements. * * THESE PARAMETERS ARE DESCRIBED WITHIN THE 'CONFIGURATION' SECTION OF THE * FreeRTOS API DOCUMENTATION AVAILABLE ON THE FreeRTOS.org WEB SITE. * * See http://www.freertos.org/a00110.html. *----------------------------------------------------------*//* USER CODE BEGIN Includes */ /* Section where include file can be added *//* USER CODE END Includes */ /* Ensure stdint is only used by the compiler, and not the assembler. */#if defined(__ICCARM__) || defined(__CC_ARM) || defined(__GNUC__) #includeextern uint32_t SystemCoreClock;#endif#define configUSE_PREEMPTION 1#define configSUPPORT_STATIC_ALLOCATION 0#define configSUPPORT_DYNAMIC_ALLOCATION 1#define configUSE_IDLE_HOOK 0#define configUSE_TICK_HOOK 0#define configCPU_CLOCK_HZ ( SystemCoreClock )#define configTICK_RATE_HZ ((TickType_t)1000)#define configMAX_PRIORITIES ( 7 )#define configMINIMAL_STACK_SIZE ((uint16_t)128)#define configTOTAL_HEAP_SIZE ((size_t)10240)#define configMAX_TASK_NAME_LEN ( 16 )#define configUSE_16_BIT_TICKS 0#define configUSE_MUTEXES 1#define configQUEUE_REGISTRY_SIZE 8#define configUSE_COUNTING_SEMAPHORES 1#define configUSE_PORT_OPTIMISED_TASK_SELECTION 1/* Co-routine definitions. */#define configUSE_CO_ROUTINES 0#define configMAX_CO_ROUTINE_PRIORITIES ( 2 )/* Set the following definitions to 1 to include the API function, or zeroto exclude the API function. */#define INCLUDE_vTaskPrioritySet 0#define INCLUDE_uxTaskPriorityGet 0#define INCLUDE_vTaskDelete 1#define INCLUDE_vTaskCleanUpResources 1#define INCLUDE_vTaskSuspend 1#define INCLUDE_vTaskDelayUntil 1#define INCLUDE_vTaskDelay 1#define INCLUDE_xTaskGetSchedulerState 1/* Cortex-M specific definitions. */#ifdef __NVIC_PRIO_BITS /* __BVIC_PRIO_BITS will be specified when CMSIS is being used. */ #define configPRIO_BITS __NVIC_PRIO_BITS#else #define configPRIO_BITS 4#endif/* The lowest interrupt priority that can be used in a call to a "set priority"function. */#define configLIBRARY_LOWEST_INTERRUPT_PRIORITY 15/* The highest interrupt priority that can be used by any interrupt serviceroutine that makes calls to interrupt safe FreeRTOS API functions. DO NOT CALLINTERRUPT SAFE FREERTOS API FUNCTIONS FROM ANY INTERRUPT THAT HAS A HIGHERPRIORITY THAN THIS! (higher priorities are lower numeric values. */#define configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY 5/* Interrupt priorities used by the kernel port layer itself. These are genericto all Cortex-M ports, and do not rely on any particular library functions. */#define configKERNEL_INTERRUPT_PRIORITY ( configLIBRARY_LOWEST_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )/* !!!! configMAX_SYSCALL_INTERRUPT_PRIORITY must not be set to zero !!!!See http://www.FreeRTOS.org/RTOS-Cortex-M3-M4.html. */#define configMAX_SYSCALL_INTERRUPT_PRIORITY ( configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )/* Normal assert() semantics without relying on the provision of an assert.hheader file. *//* USER CODE BEGIN 1 */#define configASSERT( x ) if ((x) == 0) {taskDISABLE_INTERRUPTS(); for( ;; );} /* USER CODE END 1 *//* Definitions that map the FreeRTOS port interrupt handlers to their CMSISstandard names. */#define vPortSVCHandler SVC_Handler#define xPortPendSVHandler PendSV_Handler/* IMPORTANT: This define MUST be commented when used with STM32Cube firmware, to prevent overwriting SysTick_Handler defined within STM32Cube HAL *//* #define xPortSysTickHandler SysTick_Handler *//* USER CODE BEGIN Defines */ /* Section where parameter definitions can be added (for instance, to override default ones in FreeRTOS.h) *//* USER CODE END Defines */ #endif /* FREERTOS_CONFIG_H */
cubemx的配置如下:
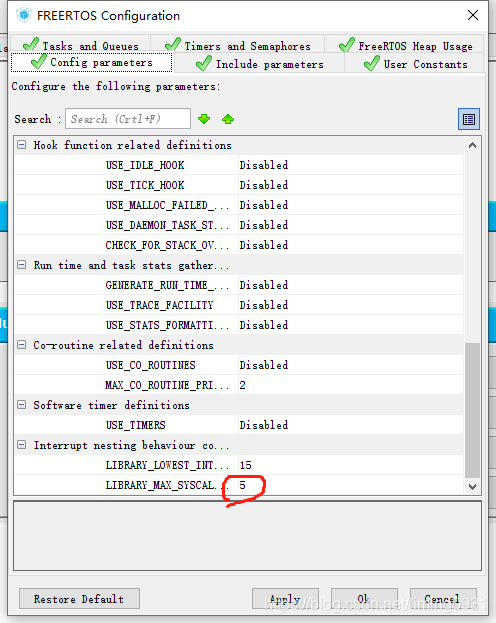
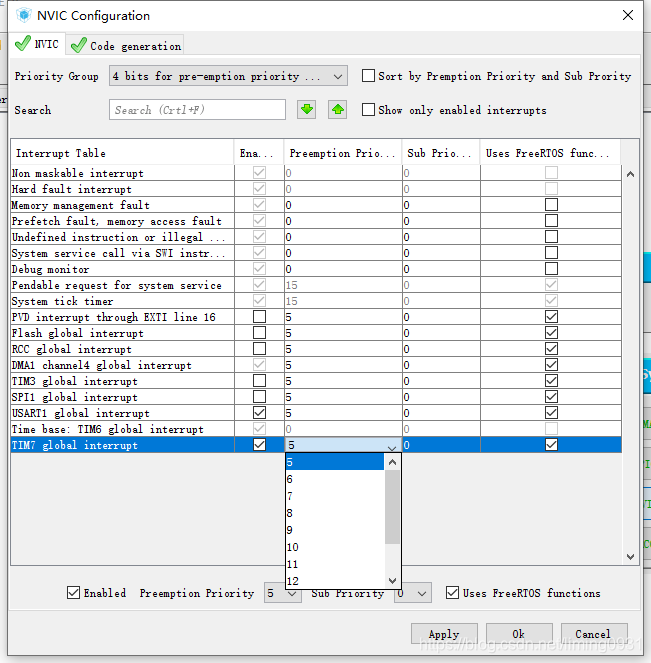
这里重点看三个宏定义
#define configMAX_PRIORITIES ( 7 )
这个宏定义的意思是任务中,只能使用0 1 2 3 4 5 6的优先级7个优先级不包括7,这里之所以是7,是因为mdk的cmsis_os.h文件里面有一个枚举
/// Priority used for thread control./// \note MUST REMAIN UNCHANGED: \b osPriority shall be consistent in every CMSIS-RTOS.typedef enum { osPriorityIdle = -3, ///< priority: idle (lowest) osPriorityLow = -2, ///< priority: low osPriorityBelowNormal = -1, ///< priority: below normal osPriorityNormal = 0, ///< priority: normal (default) osPriorityAboveNormal = +1, ///< priority: above normal osPriorityHigh = +2, ///< priority: high osPriorityRealtime = +3, ///< priority: realtime (highest) osPriorityError = 0x84 ///< system cannot determine priority or thread has illegal priority} osPriority; 这样就可以使用全部的优先级了,当然如果没有CMSIS-RTOS API的话,可以定义自己的优先级数量,在官方提供的demo中通常是5.
/* Cortex-M specific definitions. */#ifdef __NVIC_PRIO_BITS /* __BVIC_PRIO_BITS will be specified when CMSIS is being used. */ #define configPRIO_BITS __NVIC_PRIO_BITS#else #define configPRIO_BITS 4#endif/* The lowest interrupt priority that can be used in a call to a "set priority"function. */#define configLIBRARY_LOWEST_INTERRUPT_PRIORITY 15/* The highest interrupt priority that can be used by any interrupt serviceroutine that makes calls to interrupt safe FreeRTOS API functions. DO NOT CALLINTERRUPT SAFE FREERTOS API FUNCTIONS FROM ANY INTERRUPT THAT HAS A HIGHERPRIORITY THAN THIS! (higher priorities are lower numeric values. */#define configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY 5/* Interrupt priorities used by the kernel port layer itself. These are genericto all Cortex-M ports, and do not rely on any particular library functions. */#define configKERNEL_INTERRUPT_PRIORITY ( configLIBRARY_LOWEST_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )/* !!!! configMAX_SYSCALL_INTERRUPT_PRIORITY must not be set to zero !!!!See http://www.FreeRTOS.org/RTOS-Cortex-M3-M4.html. */#define configMAX_SYSCALL_INTERRUPT_PRIORITY ( configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )
截图红圈即
#define configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY 5的宏定义#define configMAX_SYSCALL_INTERRUPT_PRIORITY ( configLIBRARY_MAX_SYSCALL_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )
这个宏定义的意思是:在nvic中的外设中断的优先级一般来讲,如果在中断函数中要使用freertos的api就只能将优先级设置为5-15,0-4是不允许的,除非0-4的中断优先级的中断函数中不适用任何freertos的api
#define configKERNEL_INTERRUPT_PRIORITY ( configLIBRARY_LOWEST_INTERRUPT_PRIORITY << (8 - configPRIO_BITS) )
这个宏定义的意思是:接通将pendsv systick的优先级设置为最低,在stm32f103中就是15.
configPRIO_BITS这个值是4,因为stm32F1只是用了高四位的。下面截图是stm32f1的内核文档里面的,stm32是裁剪过的。
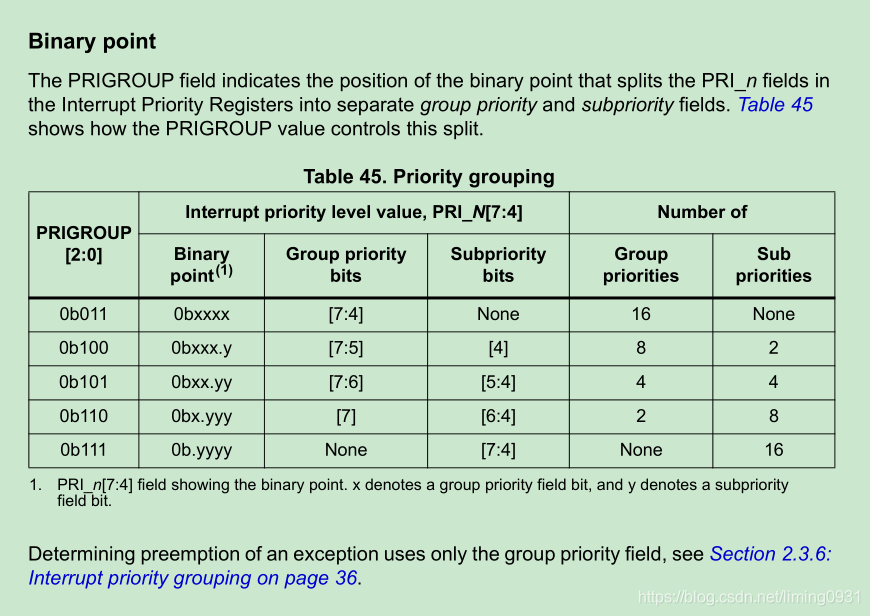
完整的优先级分组如下表所示:
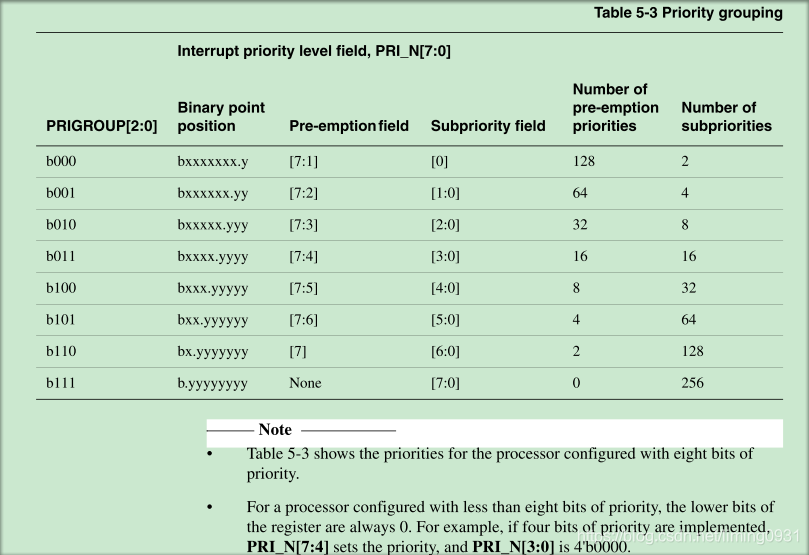
转载地址:http://prevz.baihongyu.com/